Precalculus

Topic 1: Functions

1.1     Relations

An ordered pair of two elements is called relation. The first element of the ordered pair is the object and a set of objects is called the domain of the relation. The second element of the ordered pair is the image and a set of images is called the range of the relation.

There are four types of relations, namely one-to-one, many-to-one, one-to-many and many-to-many relations.

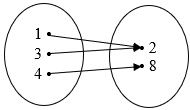
Example 1

Relation = {(1, 2), (3, 5), (4, 8)}

Domain = {1, 3, 4}

Range = {2, 5, 8}
Since one object has one and only one image and vice versa, thus this is a one-to-one relation.

Example 2

Relation = {(1, 2), (3, 2), (4, 8)}

Domain = {1, 3, 4}

Range = {2, 8}

Since one object has one and only one image while one image has at least one object, thus this is a many-to-one relation.

Example 3

Relation = {(1, 2), (1, 5), (4, 5)}

Domain = {1, 4}

Relation = {2, 5}

Since one object has at least one image and one image has at least one object, thus this is a many-to-many relation.

1.2     Functions

A special relation that matches an object to one and only one image is called a function.

Example 4
State the domain and the range of each of the following relations. Determine whether the relation is a function.

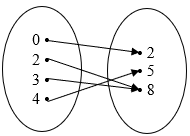
a) {(0, 2), (2, 8), (3, 8), (4, 5)}

Domain = {0, 2, 3, 4}

Relation = {2, 5, 8}

Since each object has only one image, thus this relation is a function.

b) {(2, 0), (5, 4), (8, 2), (8, 3)}

Domain = {2, 5, 8}

Relation = {0, 2, 3, 4}

Since the object 8 has two images (i.e. 2 and 3), thus this relation is a not function.

c) y = 3x + 1 

Notice that the vertical line (simply take an ordinate, say x = 2) cuts the line (y = 3x + 1) at ONLY one point, thus this relation is a function. 

Remark: this method is called the vertical line test.

d) y = x² 

The vertical line (x = 2) cuts the curve (y = x²) at ONLY one point, thus this relation is a function.

e) y² = x 

The vertical line (x = 2) cuts the curve (y² = x) at two distinct points, this relation is NOT a function. 

In other words, one object could have MORE THAN ONE IMAGE, thus this relation is not a function.

f) 

The vertical line (x = 2) cuts the curve  at ONLY one point, thus this relation is a function. 

Note: One-to-one (Example 4 - part c and f) and many-to-one (Example 4 - part d) relations are function. 

1.3     Operations with Functions

Example 5

Determine (f + g)(x), (f – g)(x), (f • g)(x) and   for each of the following functions.

a) f(x) = 2x² + 5, g(x) = 4 + 6x – x²

b) , g(x) = x² – 2

1.4     Composite Functions

If function f maps a to b and function g maps b to c, then the resultant who maps a to c is called the composite function g◦f.